Arnaud Hirtz
Analyse DEUG 2
Université de Haute Alsace
Fonctions définies par une intégrale,
fonctions de plusieurs variables
Exercice 1
Soit
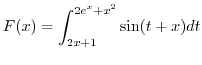 .
.
- La fonction est-elle continue ?
- La fonction est-elle dérivable ? Si oui, donner sa dérivée.
Exercice 2
Déterminer la matrice jacobienne des fonctions suivantes :
-
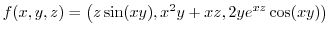
-
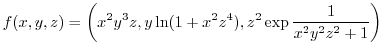
Exercice 3
Soit
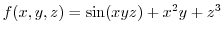 . Calculer le gradiant et le laplacien
de f.
. Calculer le gradiant et le laplacien
de f.
Exercice 4
Soit
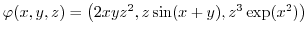 . Calculer la divergence et le rotationnel de
. Calculer la divergence et le rotationnel de 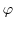 .
.
Exercice 5
Soit
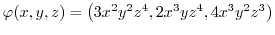 . Montrer que f dérive d'un potentiel puis trouver f
tel que
. Montrer que f dérive d'un potentiel puis trouver f
tel que
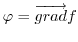 .
.
Exercice 6
Etudier la continuité et la différentiabilité de
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{x^{2}y^{2}}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. $](images/img9.gif) .
.
Exercice 7
Soit
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{xy}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img10.gif)
- Etudier la continuité de f en (0, 0).
- Etudier l'existence et la continuité des dérivées partielles.
Exercice 8
Soit
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{\sin x^{3}-\sin y^{3}}{x^{2}+y^{2}}\text{ si }%
(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img11.gif)
- Etudier la continuité de f en (0, 0).
- Etudier l'existence et la continuité des dérivées partielles.
Exercice 9
Soit
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle(x^{2}+y^{2})\sin\frac{1}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img12.gif)
- Etudier la continuité de f en (0, 0).
- Etudier l'existence et la continuité des dérivées partielles.
Exercice 10
Etudier la différentiabilité de
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{x^{3}-y^{2}}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img13.gif)
Retour à la liste des fiches
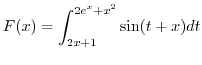
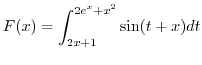
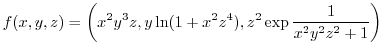
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{x^{2}y^{2}}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. $](images/img9.gif)
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{xy}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img10.gif)
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{\sin x^{3}-\sin y^{3}}{x^{2}+y^{2}}\text{ si }%
(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img11.gif)
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle(x^{2}+y^{2})\sin\frac{1}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img12.gif)
![$f(x,y)=\left\{
\begin{array}[c]{l}%
\displaystyle\frac{x^{3}-y^{2}}{x^{2}+y^{2}}\text{ si }(x,y)\neq(0,0)\\
0\text{ sinon}%
\end{array}\right. .$](images/img13.gif)